Abstract

This thesis is a compound of various works of the author and coworkers on the application of neural networks and deep learning for solving inverse problems.

The first application is in Materials Science. The development of new structural materials with desirable properties has become one of the most challenging tasks for engineers. We use Neural Networks to learn how the parameters influence the material properties and focus mainly on solving the corresponding inverse problem. Given desired properties, a material should have, we aim at finding the production parameters we need to obtain it.

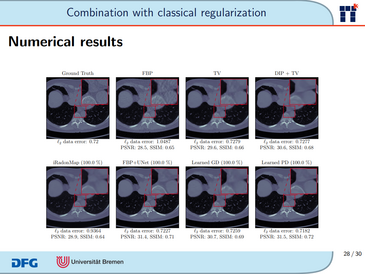
The second application is in Computed Tomography (CT), which is one of the most valuable technologies in modern medical imaging. It allows a non-invasive acquisition of the inside of the human body using X-rays. In this work, we examine the application of deep learning methods for the reconstruction of CT images in the context of a low-data regime. Firstly, we review the current challenges and existing approaches and obtain quantitative results after training them with different amounts of data. We find that the learned primal-dual method has an outstanding performance in terms of reconstruction quality and data efficiency. However, in general, end-to-end learned techniques have two issues: a) lack of classical guarantees in inverse problems and b) lack of generalization when not trained with enough data. To overcome these issues, we bring in the Deep Image Prior (DIP) approach in combination with classical regularization. The proposed methods improve the state-of-the-art results in the low data-regime.

Finally, we analyze specific network designs and discuss different interpretations of the DIP approach. We obtain theoretical results by introducing the idea of viewing these approaches as the optimization of Tikhonov functionals rather than optimizing net\-works. Additionally, we provide numerical examples that verify our findings.