Abstract

This thesis’s primary focus is on the application of deep learning methods to inverse problems. More specifically, it tries to advance the application of inverse problems for cases where straight forward supervised training is not feasible due to a lack of training data.

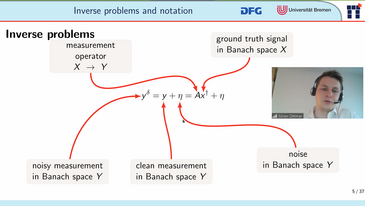
The thesis begins by introducing basic concepts concerning inverse problems, deep learning, and the latter’s application to the former. The second part of the thesis presents five papers to which the author contributed.

While the first of the papers aims to advance our understanding of neural networks by analyzing changes in properties of the data propagating through networks, the latter four are concerned with the direct application of deep learning methods to inverse problems. Two of these four papers – one more theoretical, the other focusing on magnetic particle imaging – investigate the concept of regularization by architecture, otherwise known as the deep image prior approach. Regularization by architecture is a deep learning paradigm for reconstruction that does not require any training data at all. Of the other two papers, one is concerned with training a denoiser, which, even during training, does not require any kind of ground truth data. The last of the five papers introduces a learned strongly convex penalty term based on an input-convex neural network architecture. The strong convexity allows us to formally show regularizing properties.