Jonathan Wong, Brad Ganoe, Xiao Liu, Tim Neudecker, Joonho Lee, Jiashu Liang, Zhe Wang, Jie Li, Adam Rettig, Teresa Head-Gordon, Martin Head-Gordon

J. Chem. Phys. 158, 164116 (2023)

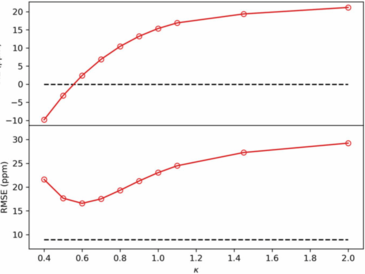
We developed and implemented a method-independent, fully numerical, finite difference approach to calculating nuclear magnetic resonance shieldings, using gauge-including atomic orbitals. The resulting capability can be used to explore non-standard methods, given only the energy as a function of finite-applied magnetic fields and nuclear spins. For example, standard second-order Møller-Plesset theory (MP2) has well-known efficacy for 1H and 13C shieldings and known limitations for other nuclei such as 15N and 17O. It is, therefore, interesting to seek methods that offer good accuracy for 15N and 17O shieldings without greatly increased compute costs, as well as exploring whether such methods can further improve 1H and 13C shieldings. Using a small molecule test set of 28 species, we assessed two alternatives: κ regularized MP2 (κ-MP2), which provides energy-dependent damping of large amplitudes, and MP2.X, which includes a variable fraction, X, of third-order correlation (MP3). The aug-cc-pVTZ basis was used, and coupled cluster with singles and doubles and perturbative triples [CCSD(T)] results were taken as reference values. Our κ-MP2 results reveal significant improvements over MP2 for 13C and 15N, with the optimal κ value being element-specific. κ-MP2 with κ = 2 offers a 30% rms error reduction over MP2. For 15N, κ-MP2 with κ = 1.1 provides a 90% error reduction vs MP2 and a 60% error reduction vs CCSD. On the other hand, MP2.X with a scaling factor of 0.6 outperformed CCSD for all heavy nuclei. These results can be understood as providing renormalization of doubles amplitudes to partially account for neglected triple and higher substitutions and offer promising opportunities for future applications.