T. van der Heide, B. Hourahine, B. Aradi, T. Frauenheim, and T. A. Niehaus

Phys. Rev. B  109, 245103 (2024)

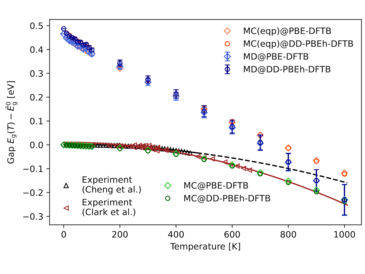
Global hybrid exchange-correlation energy functionals within generalized Kohn-Sham density functional theory have long been established as part of the standard repertoire for electronic structure calculations. Accurate electronic band structures of solids are indispensable for a wide variety of applications and should provide a sound prediction of phonon-induced band gap renormalization at finite temperatures. We employ our previously introduced formalism of general hybrid functionals within the approximate density functional tight-binding (DFTB) method to present insights into the accuracy of temperature dependent band gaps obtained by a dielectric dependent global hybrid functional. The work targets the prototypical group-IV semiconductors diamond and silicon. Following [Zacharias et al. Phys. Rev. Lett. 115, 177401 (2015)], we sample the nuclear wave function by stochastic Monte Carlo integration as well as the deterministic one-shot procedure [M. Zacharias and F. Giustino, Phys. Rev. B 94, 075125 (2016)] derived from it. The computational efficiency of DFTB enables us to further compare these approaches, which fully take nuclear quantum effects into account, with classical Born-Oppenheimer molecular dynamic (BOMD) simulations. While the quantum mechanical treatments of Zacharias et al. yield band gaps that are in good agreement with experiment, calculations based on BOMD snapshots inadequately describe the renormalization effect at low temperatures. We demonstrate the importance of properly incorporating nuclear quantum effects by adapting the stochastic approach to normal amplitudes that arise from the classical equipartition principle. For low temperatures, the results thus obtained closely resemble the BOMD predictions, while anharmonic effects become important beyond 500 K. Comparisons between DFTB parametrized from semilocal DFT, and global hybrid DFTB, suggest that Fock-type exchange systematically yields a slightly more pronounced electron-phonon interaction, and hence stronger gap renormalization and zero-point corrections.