Stefan Christian Endres, Marc Avila, Lutz Mädler
Chemical Engineeering Science 257 (2022), 117681
doi: https://doi.org/10.1016/j.ces.2022.117681
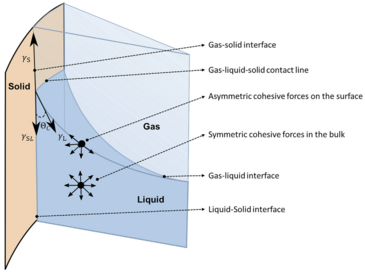
Many systems in fluid dynamics and materials science are modelled using multiphase energy balances which can be reduced to an interface, curvature-driven mechanical problem. When simulating these systems, it is desirable to understand the details and changes of the underlying micro- and mesostructures. However, conventional numerical methods formulated in Cartesian coordinates are incapable of accurately simulating many complex systems over the space and timespans of interest. In this work, we demonstrate how modern developments in the field of discrete differential geometry can be exploited to greatly reduce the computational resources required in the simulation of multiphase systems. In particular we show how local–global theorems such as the discrete Gauss-Bonnet Theorem can be used to compute the exact mean normal- and geodesic curvatures of convex interfaces in equilibrium. In addition, we provide error estimates needed for a particular mesh refinement to retain a predetermined accuracy in the simulations. Our coordinate free formulation can be applied to any data structure used for multiphysics simulations when the underlying space of the interface is manifold. In order to validate the accuracy of the formulation with physical systems, it was applied to test cases of capillary rise, particle–particle bridges and a Sessile microdroplet system with near-exact results (subject to floating-point errors).
@ 2022 The Author(s) licensed under CC BY 4.0